1. 八年级数学兴趣小组组织了以“等积变形”为主题的课题研究．

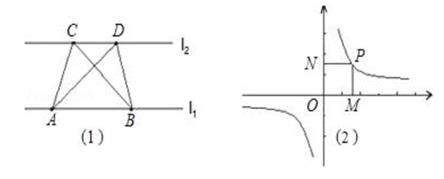
    第一学习小组发现：如图(1)，点A、点B在直线l₁上，点C、点D在直线l₂上，若l₁∥l₂ ， 则S_△ABC=S_△ABD；反之亦成立．

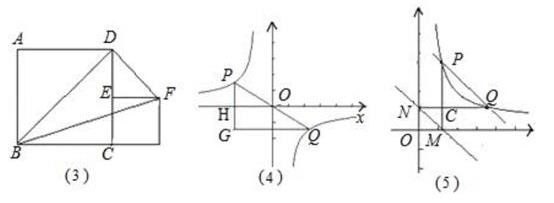
第二学习小组发现：如图(2)，点P是反比例函数y= 上任意一点，过点P作x轴、y轴的垂线，垂足为M，N，则矩形OMPN的面积为定值|k|．请利用上述结论解决下列问题：

1. （1） 如图(3)，四边形ABCD与四边形CEFG都是正方形，点E在CD上，正方形ABCD边长为2，则S_△BDF=．
   
3. （2） 如图(4)，点P、Q在反比例函数y= 图象上，PQ过点O，过P作y轴的平行线交x轴于点H，过Q作x轴的平行线交PH于点G，若S_△PQG=8，则S_△POH=，k=．
   
5. （3） 如图(5)点P、Q是第一象限的点，且在反比例函数y= 图象上，过点P作x轴垂线，过点P作y轴垂线，垂足分别是M、N，试判断直线PQ与直线MN的位置关系，并说明理由．